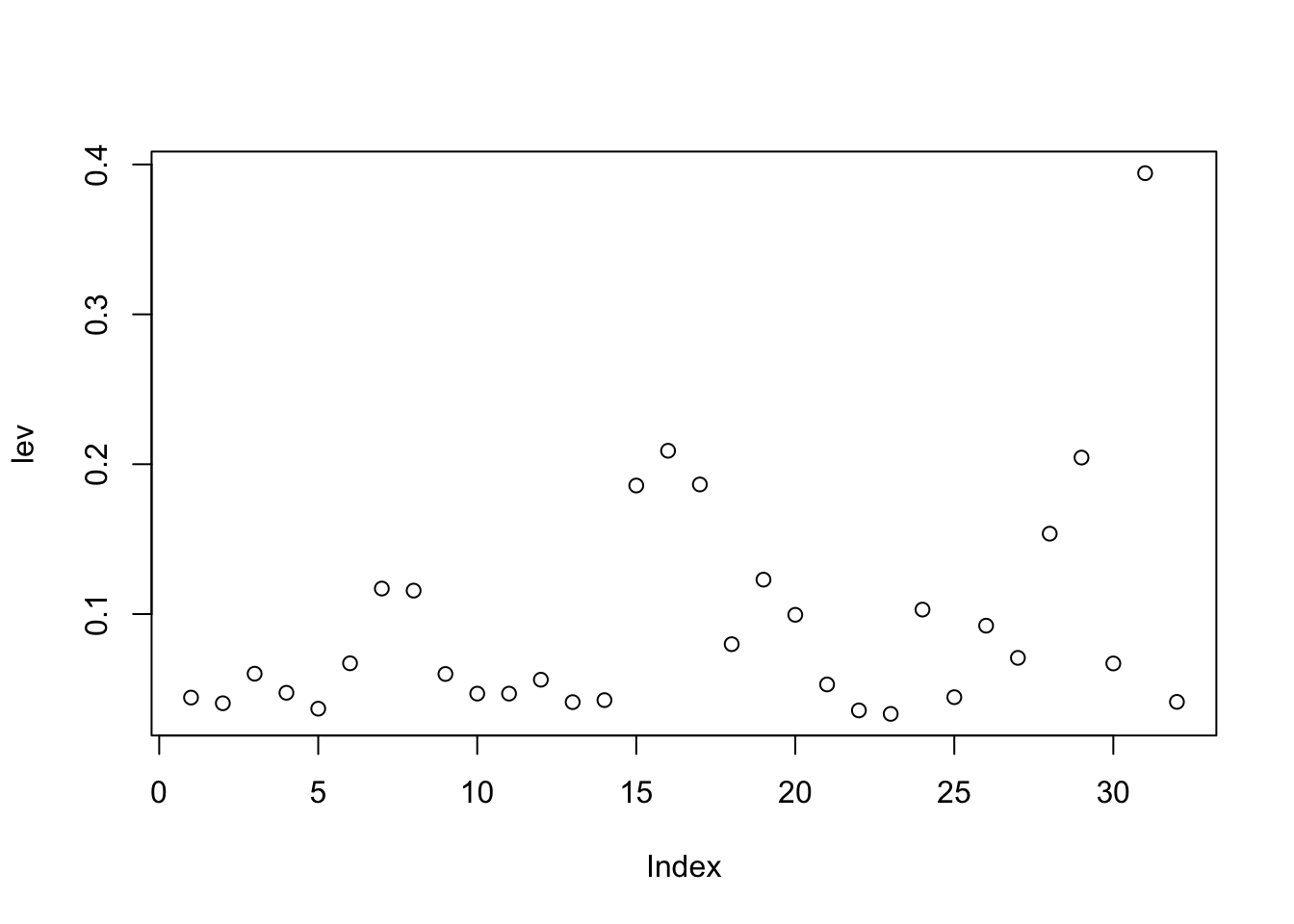
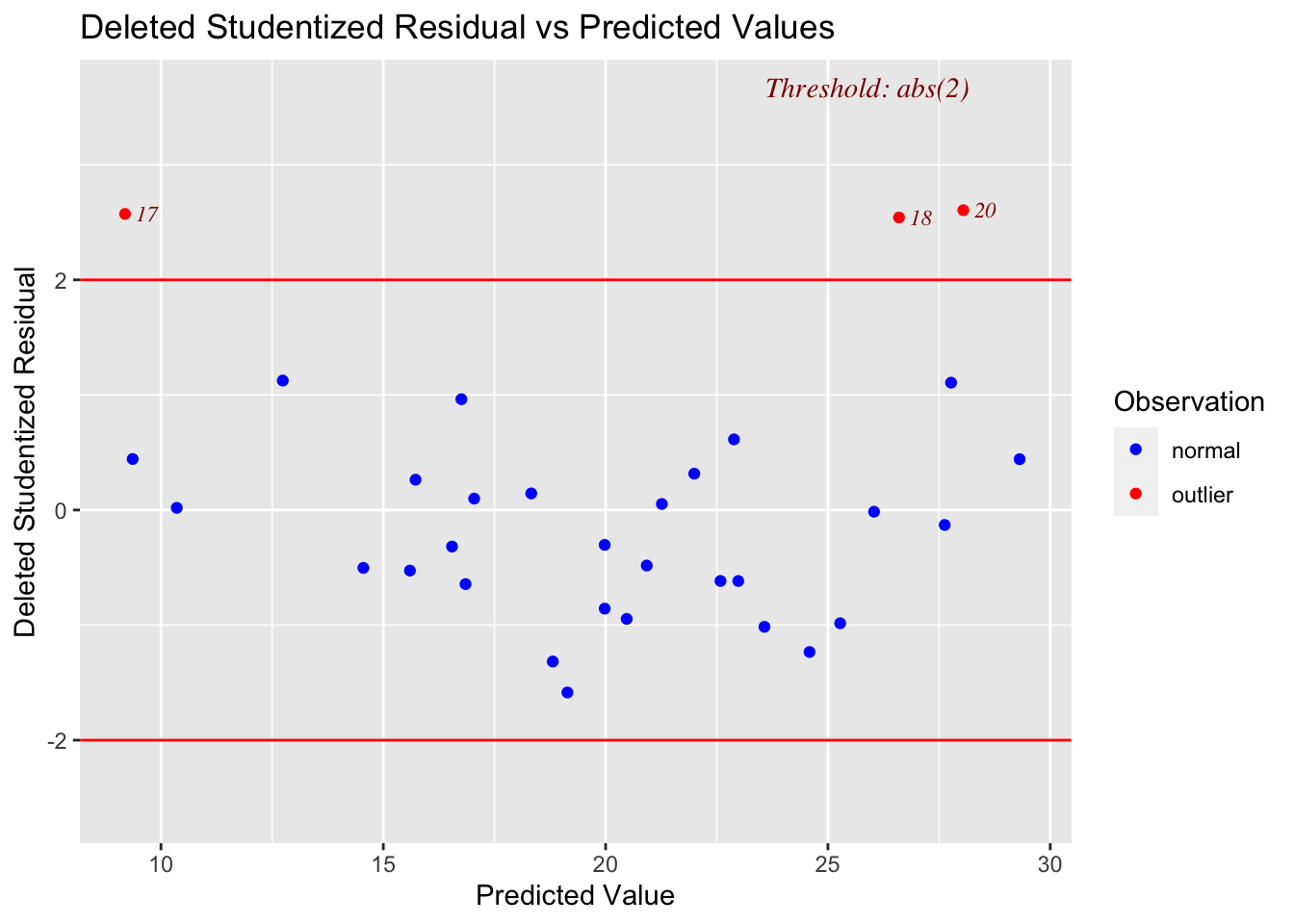
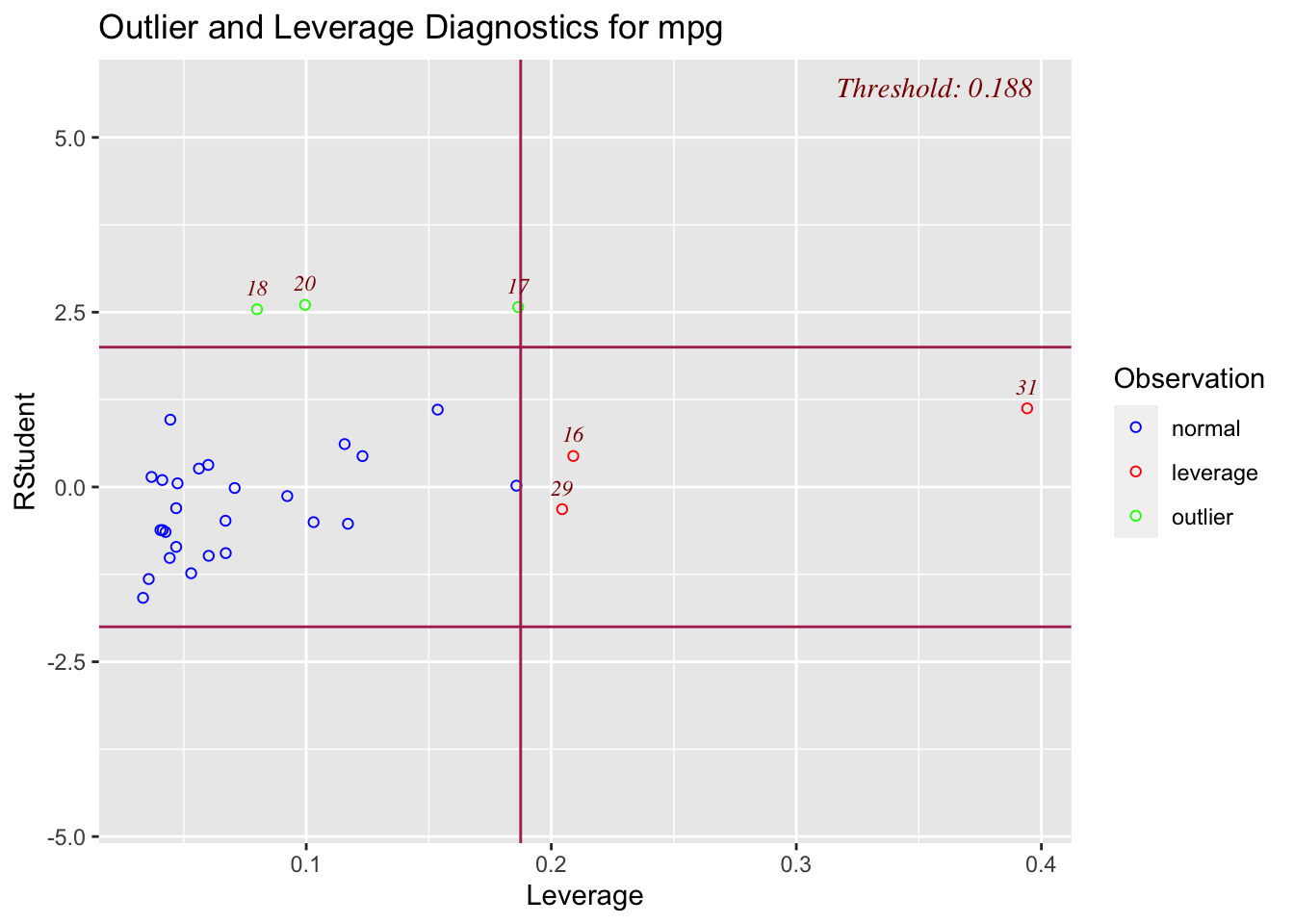
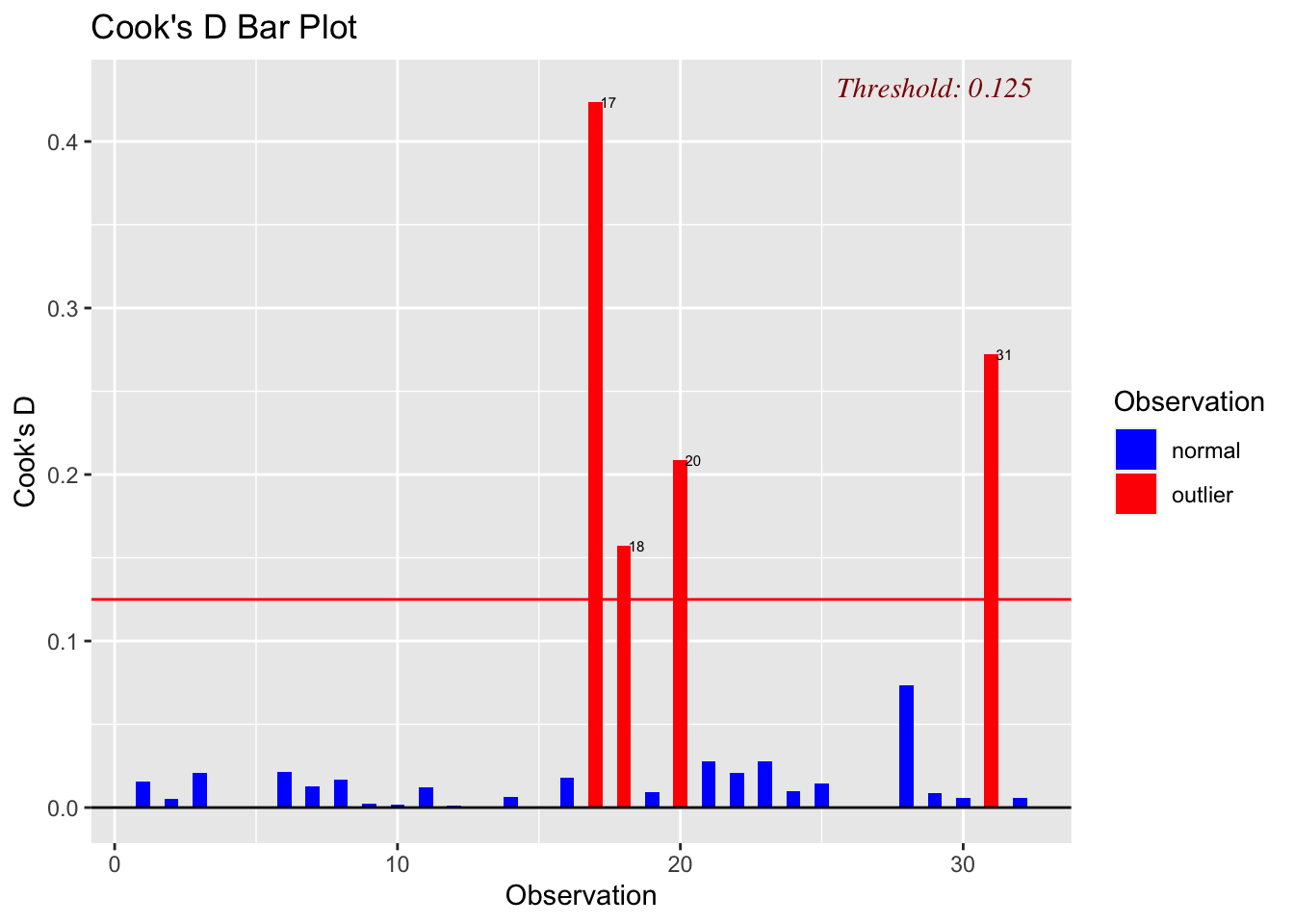
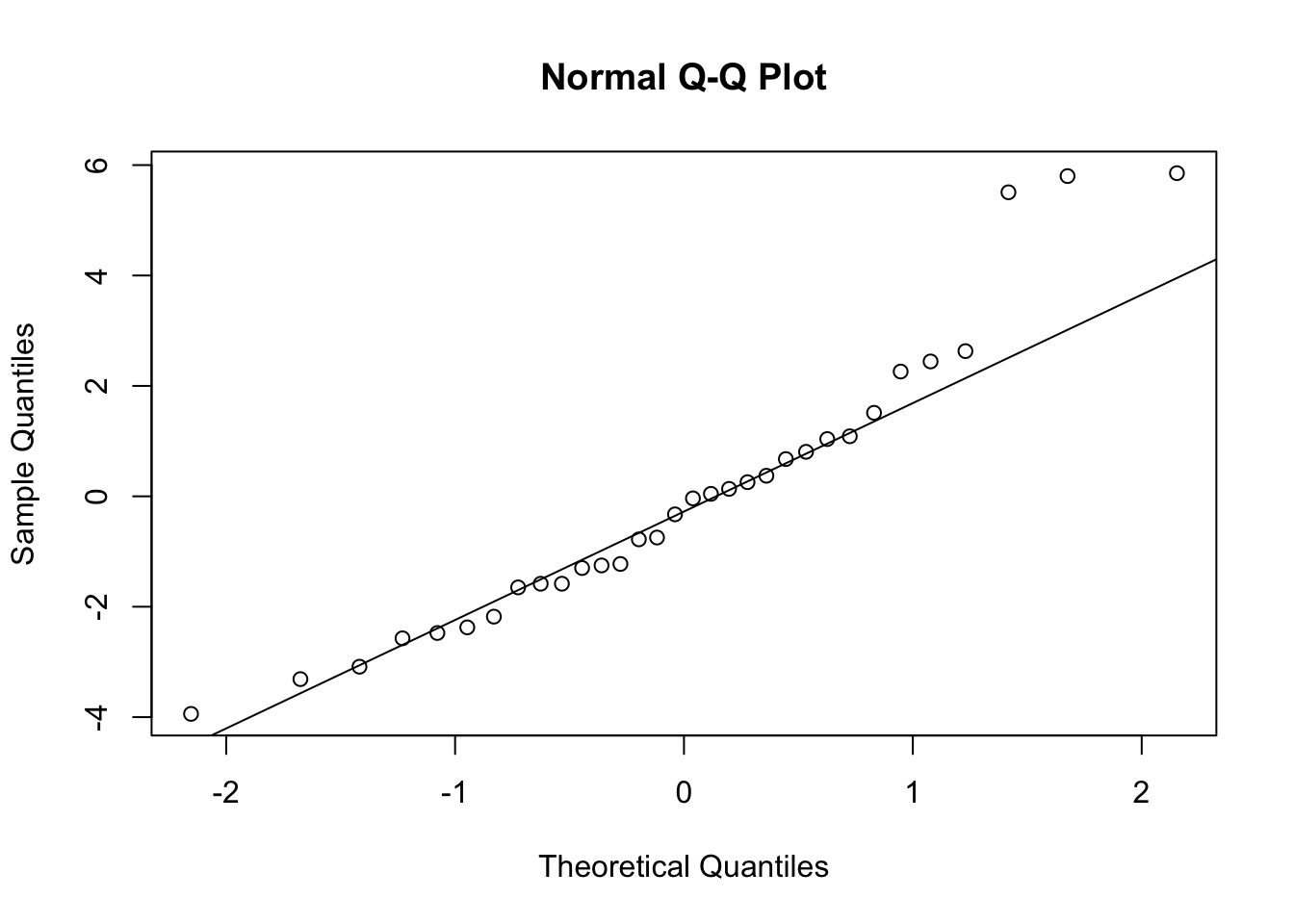
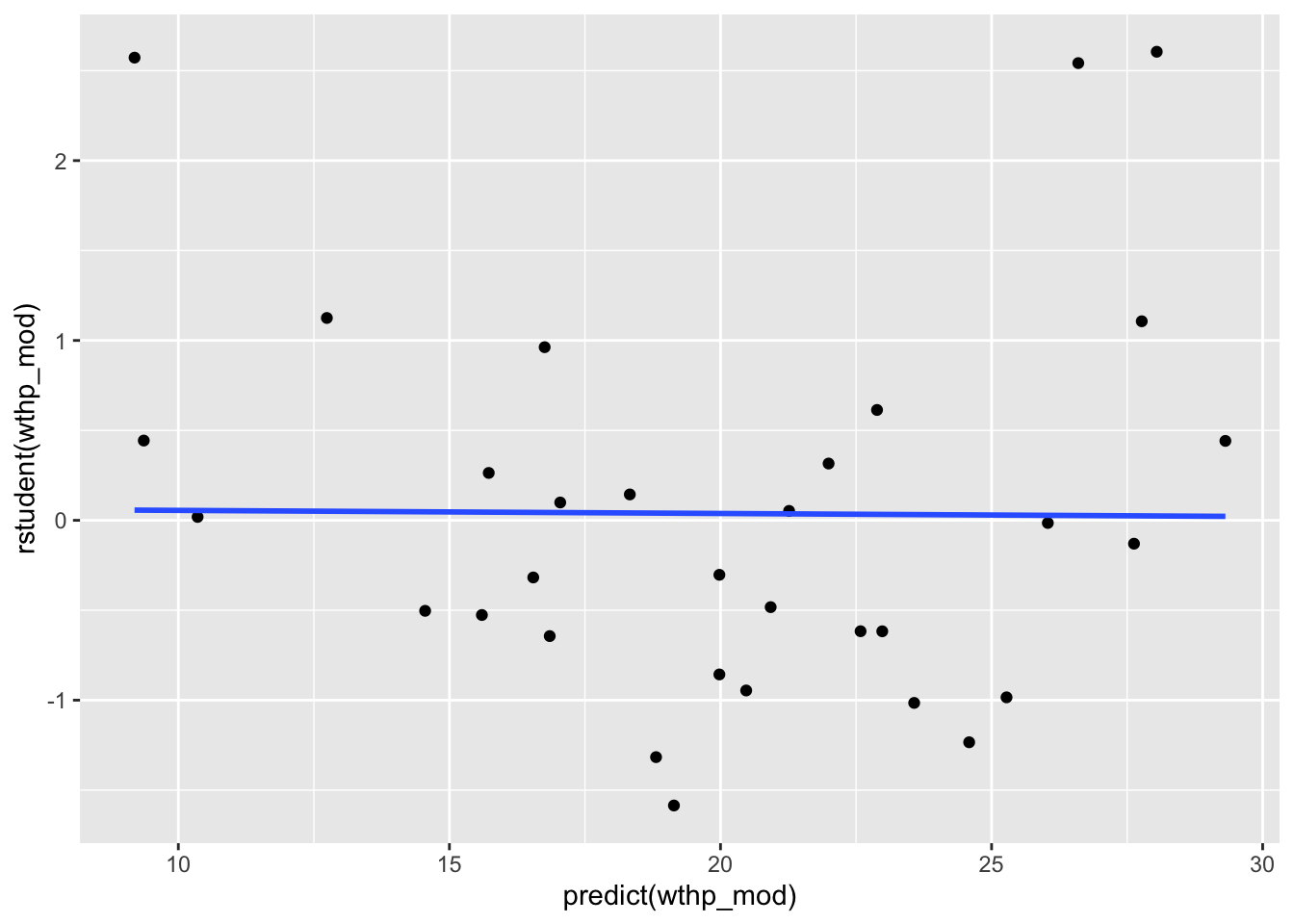
3.1 Main Effects
The lm() function makes adding additional predictors to our regression formulas incredibly easy. We can simply just add the predictor (pun intended) to our model, as shown below.
wthp_mod <- lm(mpg ~ wt + hp, data = mtcars)
summary(wthp_mod)##
## Call:
## lm(formula = mpg ~ wt + hp, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.941 -1.600 -0.182 1.050 5.854
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.22727 1.59879 23.285 < 2e-16 ***
## wt -3.87783 0.63273 -6.129 1.12e-06 ***
## hp -0.03177 0.00903 -3.519 0.00145 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.593 on 29 degrees of freedom
## Multiple R-squared: 0.8268, Adjusted R-squared: 0.8148
## F-statistic: 69.21 on 2 and 29 DF, p-value: 9.109e-12We can see from the summary above that this model includes both wt and hp as predictors in our model. We can also see that the reported t-values (and their respective p-values) for each predictor have changed, as we might expect from having multiple predictors in the model.
We may wish to run a simple model comparison to see if the trade-off between the added complexity of our additional terms and the increase in PRE (Proportional Reduction in Error; Multiple R-squared) is worth it. We can do this with the anova() function.
anova(wt_mod, hp_mod, wthp_mod)## Analysis of Variance Table
##
## Model 1: mpg ~ wt
## Model 2: mpg ~ hp
## Model 3: mpg ~ wt + hp
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 30 278.32
## 2 30 447.67 0 -169.35
## 3 29 195.05 1 252.63 37.561 1.12e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1From this output, we can see that the model including both predictor main effects is a significant improvement over the single-term models.